[백준 알고리즘]2839번 설탕 배달 문제 그리디 알고리즘으로 풀이

 
 
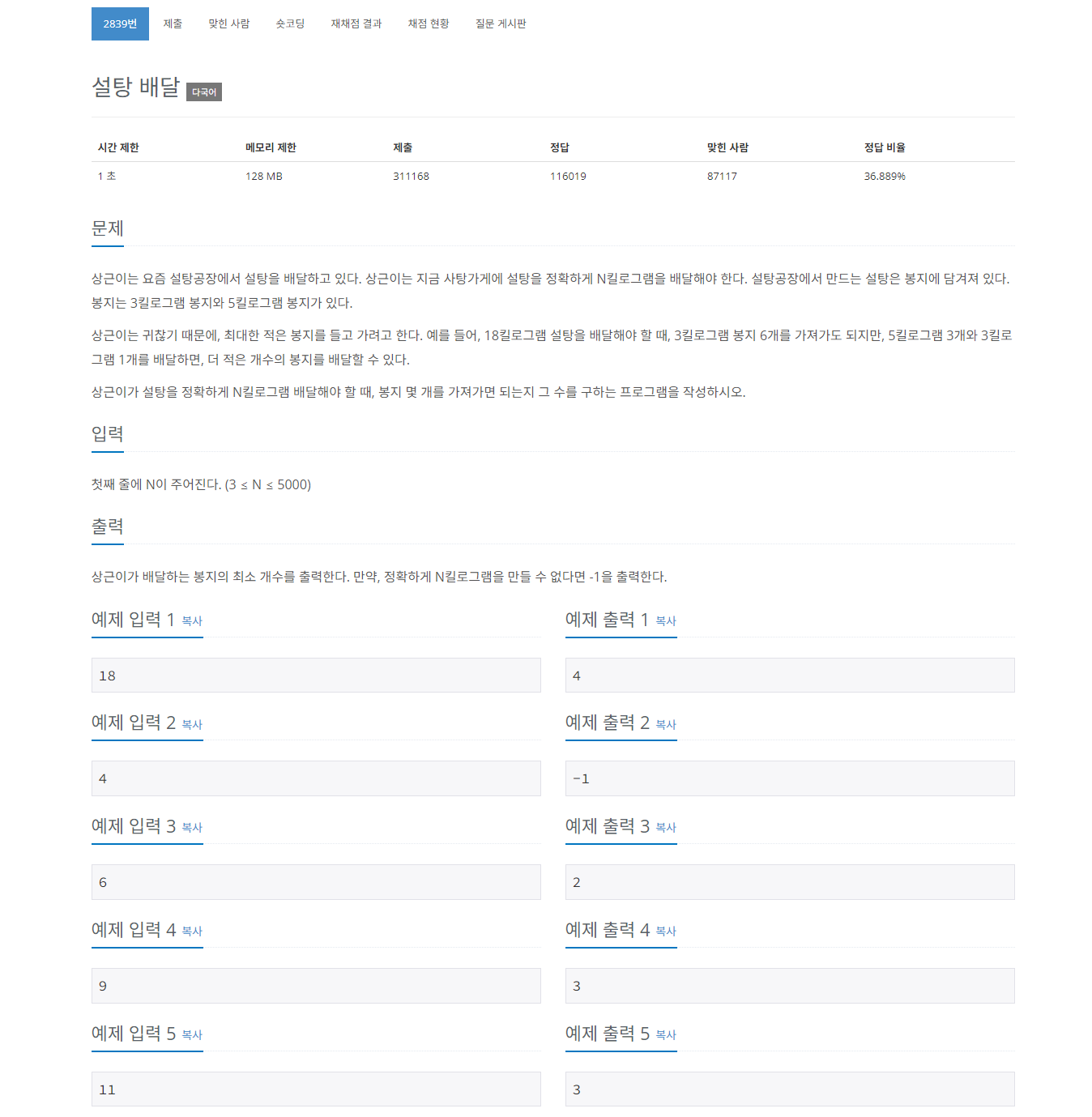
먼저 입력 가능한 N을 그림으로 표현하면 다음과 같다.

 
 
이때, 배달할 설탕 봉지 수를 구하기 위해 사용할 수 있는 연산에는 4가지 있다.

• 3으로 나눈다
• 5로 나눈다 
• 3을 뺀다
• 5를 뺀다

 
 

1. N이 3의 배수일 때

 
먼저 N이 3의 배수인 경우를 그림으로 나타내면 다음과 같다. 이때 N으로부터 설탕 봉지 수를 구하기 위해 선택할 수 있는 연산은 다음 2가지이다.

 

• 3으로 나눈다
• 3을 뺀다

 

이 중 연산의 효율성 측면으로만 따졌을때 가장 먼저 선택해 볼 수 있는 방법은 3으로 나누는 연산이다. 하지만 이 경우 18 ÷ 3 = 6이 되므로 예제 입력 1의 출력 조건을 만족할 수 없다. 반면, 3을 빼는 연산을 진행하는 경우 18 - 3 = 15가 되어 5를 이용한 연산이 가능해지고 예제 입력 1의 출력 조건도 만족시킬 수 있게 된다. 더불어 예제 입력 3과 예제 입력 4의 출력 조건 역시 만족시킬 수 있다. 따라서 이 경우 3을 빼는 연산을 하는 것이 더 합리적이라고 할 수 있다.
 
 

2. N이 5의 배수일 때

 
다음은 N이 5의 배수인 경우이다. N이 5의 배수인 경우에는 선택 할 수 있는 연산은 다음 2가지가 있다.

 

• 5로 나눈다
• 5를 뺀다

 

다만, 이경우 더 효율적으로 N을 줄여나갈 수 있는 것은 N을 5로 나누는 연산이다. 그러므로 N이 5의 배수라면 5로 나누는 연산을 진행 것이 더 적합하다.
 
 
 

3. N이 3과 5의 공배수일 때

 
이번엔 N이 3과 5의 공배수인 경우를 생각해 보자. 이 경우 다음과 같이 4가지 연산이 모두 가능하다.

 

• 3으로 나눈다
• 5로 나눈다
• 3을 뺀다
• 5를 뺀다

 

하지만 3과 관련된 연산으로 설탕 봉지수를 최소화기란 불가능하다. 그렇기 때문에 이 경우 5와 관련된 연산을 진행하는 쪽으로 생각해야 한다. 5의 배수인 경우는 앞서 언급되었듯이 5로 나누는 연산이 가장 효율적이다. 따라서 이 경우도 마찬가지로 5로 나누는 연산을 진행하도록 해야 한다.
 
 

4. 그 외의 경우(N이 3의 배수도 아니고 5의 배수도 아닌 경우)

 
이제 N이 3의 배수도 아니고 5의 배수도 아닌 경우를 생각해 보자.
 
 

4-1. 15개의 간격으로 분할해서 규칙 찾기

앞서 언급된 3의 배수도 아니고 5의 배수도 아닌 경우를 15개의 간격으로 분할하면 다음 그림과 같다.

 
이 그림에서 보는 바와 같이 N이 3의 배수도 아니고 5의 배수도 아닌 경우에도 특정한 규칙을 갖는다는 것을 볼 수 있다. 그것은 N에 15를 더하면 그 결과 역시 3의 배수도 아니고 5의 배수도 아닌 값이 나온다는 것이다. 이것은 바꿔 말하면 N에서 15를 빼면 그 결과 역시 3의 배수도 아니고 5의 배수도 아닌 값이 나오게 된다는 것이다. 그리고 여기서 주목할 점이 바로 15를 빼는 것이다. 이 '15를 빼는 연산' 자체는 선택지에 존재하지 않는다. 하지만 앞서 언급한 4가지 연산 중 하나를 중첩 수행함으로써 구현은 가능하다. 바로 다음 2가지 연산이다.

 

 

• 3을 뺀다
• 5를 뺀다

 

이때 '3을빼는 연산'은 5회 중첩 수행되어야 하고, '5를 빼는 연산'은 3회 중첩 수행되어야 한다는 점에서 효율성을 따졌봤을때  '5를 빼는 연산'을 선택하는 것이 더 합리적일 것이다. 이렇게 하면 예제 입력 5의 출력 조건을 만족하는 결과를 얻을 수 있다.
 
 

4-2. N이 5 미만 일 때

 
그런데 만약 N이 5 미만이라면 어떻게 해야할까? 이때는 앞서 언급한 5를 빼는 연산을 해도 음수가 되므로 적절한 해를 구할 수 없다. 따라서 이 경우에 한해서는 설탕 봉지 수를 -1로 초기화해 주면 된다. 이렇게 하면 예제 입력 2의 출력 조건까지 만족시킬 수 있다.
 
 

5. 코드 구현

 
지금까지의 설명을 Java 코드로 작성하면 다음과 같다.

...

public class SugarDelivery {
	
	public static void main(String[] args) {
		Scanner input = new Scanner(System.in);
		int N = input.nextInt();
		
		
		int minBag = 0;
		
		
		while(0<N) {
			if(N%3==0 && N%5==0) {//3과 5의 공배수인 경우 5로 나누기(ex 15
				minBag += N/5;
				N %= 5;
			}else if(N%5==0) {//5의 배수인 경우 5로 나누기
				minBag += N/5;
				N %= 5;
			}else if(N%3==0) {//3의 배수인 경우 3을 빼기
				N -= 3;
			}else {//그 외의 경우 5를 빼기(ex 1, 2, 4, 7, 8, 11, ...
				if(N<5) {//이때 N < 5이면, 즉 1,2,4 일땐 해를 구할 수 없으므로 -1
					minBag = -1;
					break;
				}
				N-=5;
				minBag += 1;
			}
		}
		System.out.println(minBag);
		input.close();
	}

}

 
 

6. 시간 복잡도 분석

마지막으로 이 알고리즘의 시간 복잡도를 분석해 보았다. 간단하게 표로 작성해 보면 다음과 같다.

N	선택한 연산	최적의 경우	최악의 경우
N이 3의 배수일 때	3 빼기	O(1)	O(N)
N이 5의 배수일 때	5로 나누기	O(1)	O(1)
N이 3과 5의 공배수일 때	5로 나누기	O(1)	O(1)
그 외	5 빼기	O(1)	O(N)

 
 
 
 
[출처]
https://www.acmicpc.net/problem/2839 : [2839번 설탕 배달] 문제